◇ 영재고 도전하기
>>>>> 문 제
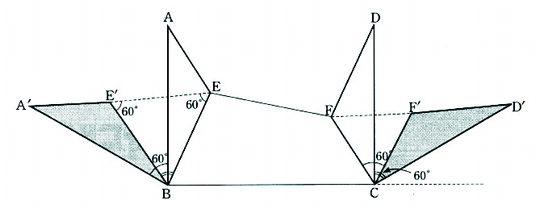
아래의 그림과 같이 한 변의 길이가 1인 정사각형 ABCD의 내부에 점 E와 F를 잡을 때, AE+EB+EF+DF+FC의 최솟값을 구하여라.
>>>>> 임쌤의 강의
기하분야의 문제이다. 지난주에 이어지는 최단거리 문제이다. 이번 주에는 평행이동, 대칭이동이 아닌 회전이동을 해야 하는 문제이다. 제시한 두 문제 모두 해석학적인 접근은 바람직하지 하지 않다. 정답률이 높지 않은 문제이다. 하지만 빈번하게 출제되는 문제이며 회전이동이 필요하다는 발상만 있었으면 쉽게 접근이 가능하다. 보통은 60°의 각도로 회전 이동을 한다. 60°로 회전이동하게 되면 세 변의 길이가 모두 같은 정삼각형이 나오기 때문이다. 역시 회전 이동을 하게 되면 원래 도형과 변환된 도형은 합동이다. 역시 마지막으로는 삼각부등식에 의해 고정된 두 점사이의 직선거리가 최단거리가 된다. 항상 유사한 도형문제를 접할 때, 세 가지 변환(평행,대칭,회전)을 반드시 유념하기를 바란다.
>>>>> 문 제 풀 이
[기하] 다음 그림과 같이 △AEB와 △DFC를 각각 좌, 우로 60°씩 회전하면 다음 그림과 같다.
AE+EB=A`E`+E`B=A`E`+E`E,
DF+FC=D`F`+F`C=D`F`+F`F
이므로
AE+EB+EF+DF+FC = A`E`+E`E+EF+FF`+F`D`
따라서 주어진 문제는 `고정된 두 점 A`,D`으로부터 A`E`+E`E+EF+FF`+F`D`의 값이 최소가 되도록 두 점 E,F를 사각형 내부에 정하는 문제` 로 바꾸어 생각할 수 있다.
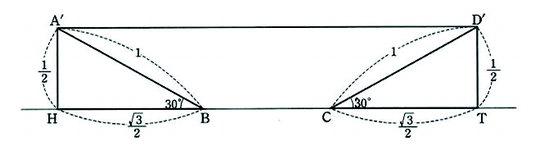
한편, 네 점 E`,E,F,F` 이 모두 A`D`위의 점이고, ∠AEE`= 60°, ∠DEF`= 60°를 만족할 때, 주어진 길이의 최솟값은 A`D`이므로 아래의 그림에서 A`D`의 길이를 구하면
·2+1= +1
이 된다.
정답: +1(난이도상)
>>>>> 유 사 문 제
그림은 한 변의 길이가 6인 정사각형 ABCD이다.
□ABCD의 내부의 한 점을 E라 할 때, (BE+CE+DE)10의 최솟값을 구하여라.
>>>>> 문 제 풀 이
그림과 같이 △CDE를 점 C를 중심으로 시계 방향으로 60°회전이동하면 △CFG가 되고 △CGE는 정삼각형이 된다.
∴BE+CE+DE=BE+EG+GF≥BF
따라서 (BE+CE+DE)10의 최솟값은 BF10이다.
점 F에서 BC의 연장선에 내린 수선의 발을 H라 하면 CF=CD=6,
∠BCF=∠BCD+∠DCF=90°+60°= 150°이므로
∠FCH=180°-150°= 30°
△FCH에서 FH=3, CH=3
∴BF10=(BC+CH)10+(FH)10=(6+3 )10+310=72+36 이다.
정답: 72+36 (난이도중)
◇ 중등 수학경시 도전하기
>>>>> 문 제
1≤χ≤y≤z≤4를 만족하는 임의의 실수 χ,y,z에 대하여
(χ-1)10+( -1)10+( -1)10+( -1)10의 최솟값을 구하여라.
>>>>> 임쌤의 강의
대수 분야의 문제이다. 코시-슈바르츠 부등식과 산술기하의 절대부등식을 이용하는 문제이다. 경시수학에서 반드시 출제된다고 생각하고 준비해야 하는 내용이다. 위에 제시한 문제는 코시-슈바르츠 부등식과 산술기하의 절대부등식을 적재적소에 적용해야 풀리는 문제이다.
(a10+b10)(χ10+y10)≥(aχ+by)10 (a,b,χ,y는 실수, 등호는 = 일 때, 성립한다.)
(a10+b10+c10)(χ10+y10+z10)≥(aχ+by+cz)10(a,b,c,χ,y,z는 실수, 등호는
= = 일 때, 성립한다.)
위의 두 부등식이 코시-슈바르츠 부등식의 가장 간단한 대수식이다. 증명방법은 다양한 방법이 있으며 위의 두 부등식은 사칙연산만으로도 간단하게 증명된다. 다른 수학 분야에서도 또 다른 형태로 표현된다. 또한 기하적으로는 길이와 각 사이의 관계를 연결해주는 매우 중요한 부등식이기도 하다. 수학분야에서 중요한 위치를 차지하며 그러한 이유로 입시에서도 반드시 출제된다.
χ+y≥2 (χ>0,y>0 등호는 χ=y일 때 성립한다.)
χ+y+z≥3 (χ>0,y>0,z>0 등호는 χ=y=z일 때 성립한다.)
위의 두 부등식이 산술기하의 절대부등식의 간단한 대수식이다. 위의 두 부등식은 대수적으로 간단하게 증명된다. 일반적으로 산술기하의 절대부등식으로 풀리는 문제들은 코시-슈바르츠 부등식으로도 해결가능하다. 또한 산술기하의 기하적인 증명 방법은 자주 출제되었으며 아래의 유사문제1에 제시하였다. 자유자재로 적용할 수 있도록 연습해야 하는 문제 유형이며 고난이도 문제까지도 반드시 풀어내야 한다.
>>>>> 문 제 풀 이
코시-슈바르츠 부등식에 의하여
(110+110+110+110) (χ-1)10+( -1)10+( -1)10+( -1)10
≥ (χ-1)10+( -1)10+( -1)10+( -1)10 이다.
또한, 산술평균, 기하평균의 관계에 의하여 다음의 부등식이 각각 성립한다.
χ+ ≥2 , + ≥ ,2 + ≥ 4
따라서, (χ-1)10+( -1)10+( -1)10+( -1)10 ≥ (4 -4)10=4( -1)10 이다.
그리고 등호는 χ= , y=2, z=2 일 때 성립하므로 최솟값은 4( -1)10이다.
정답: 4( -1)10 (난이도중)
>>>>> 유 사 문 제 1
그림과 같이 중심이 A이고 지름의 길이가 a인 원과 중심이 B이고 지름의 길이가 b인 원이 서로 외접한다. 그림을 이용하여 a≥b>0일 때, 부등식 ≥ 가 성립함을 증명하시오.
>>>>> 문 제 풀 이
AB는 두 원의 반지름의 합이므로 이다.
두 원의 공통외접선과의 교점을 각각 C,D라 하고, 점 B에서 점 C를 지나는 지름에 내린 수선의 발을 E라고 하면 CE=BD이므로 AE=AC-CE= 이다.
∴ BE= = - = 이다.
AB≥BE 이므로 ≥ 이다
>>>>> 유 사 문 제 2
한 변의 길이가 1㎝인 직사각형 ABCD를 서로 수직인 두 직선으로 나누어 4개의 작은 직사각형을 만들 수 있다. 그 중 세 개의 직사각형의 넓이는 1㎠ 보다 작지 않고, 나머지 한 개의 직사각형의 넓이는 2㎠보다 작지 않다고 한다. 이 직사각형의 다른 한 변의 길이 χ의 최솟값을 구하여라.
>>>>> 문 제 풀 이
이 문제는 코시-슈바르츠 부등식, 산술기하평균의 절대부등식 둘 다 풀이가 가능한 문제이다. 코시-슈바르츠 부등식을 이용한 풀이이다.
a>0, b>0, a+b=1, c>0, d>0, c+d=χ
χ=(a+b)(c+d)≥ ( + )10≥(1+ )10 정답 : (1+ )10(난이도 상)
<저작권자ⓒ대전일보사. 무단전재-재배포 금지>