△문제1

`반복 숫자`란 순서를 뒤집어 보아도 똑같이 읽히는 숫자를 말한다. 예를 들면 23732와 3773은 반복숫자이다. 10 이상 10000 이하의 자연수 중에서 반복 숫자는 몇 개인가?

[풀이]

1) 두 자리 수는 11, 22, ···, 99의 9개가 있다.

2) 세 자리 수는 처음과 끝자리의 수가 같고(0은 제외해야 함), 가운데 숫자는 어떤 것이든 상관없으므로, 9x 10= 90(개)가 있다.

3) 네 자리 수는 처음과 끝자리(역시 0은 제외), 그리고 두 번째와 세 번째 자리의 숫자가 각각 같아야 한다. 9x 10=90(개)

따라서 10과 10000 사이에는 9+90+90=189(개)의 반복 숫자가 있다.

　답 : 189(개)

△문제2

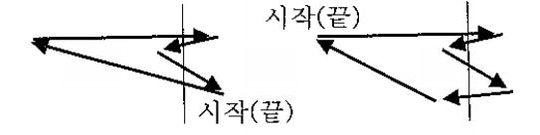
11개의 선분을 연결해서 시작하는 점과 끝나는 점이 서로 만나도록 닫힌 길(폐다각형의 변)을 만든다고 하자. 한 개의 직선 을 그어서 11개의 모든 선분과 만나도록 할 수 있는가? 있는지 없는지 답하고 그 이유도 설명하라. (단, 직선 이 선분들의 꼭짓점과 만나게 해서는 안 된다.)

[풀이]

불가능하다. 여러분이 개미처럼 작은 곤충이 되어서 폐다각형의 한 꼭짓점에서 출발하여 폐다각형의 변을 따라서 시계방향으로 돌면서 여행한다고 생각해보자. 그러면 각 변의 어떤 점에서 직선 을 만날 때마다 직선 에 의하여 갈라진 영역을 반드시 넘나들게 된다. 즉, 아래 그림처럼 출발점에서 시작하여 출발점이 있는 영역까지 다시 되돌아오려면 짝수 번 직선 과 만나야만 한다. 그러려면 다각형의 변의 개수가 짝수이어야 한다. 그런데 문제의 다각형은 홀수 개의 변(11개)으로 이루어져 있으므로 불가능함을 알 수 있다.

　답 : 불가능하다.

△문제3

4개의 톱니바퀴를 다음 그림처럼 원 모양으로 서로 연결하였다. 이들 가운데 어느 한 톱니바퀴를 돌리더라도 모두 같이 맞물려 돌아간다. 그렇다면 2006개의 똑같은 톱니바퀴를 위와 마찬가지 방법으로 원 모양으로 서로 연결해 놓을 때, 어느 한 톱니바퀴를 돌리면 다른 톱니바퀴들도 모두 같이 돌아가는가? 만약 톱니바퀴가 2007개라면 어떻겠는가?(단, 톱니들의 크기와 간격은 모두 같다.)

[풀이]

2006은 짝수이므로 돌아간다. 2006개의 똑같은 톱니바퀴를 위와 마찬가지 방법으로 서로 연결하면 잘 돌아간다. 하지만 2007개의 경우는 전혀 돌아가지 않는다.

　답 : 풀이 참조

<저작권자ⓒ대전일보사. 무단전재-재배포 금지>