▶ 문 제
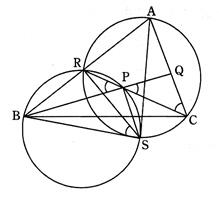
삼각형 ABC의 내부의 한 점 P에서, AC와 BP의 연장선과의 교점을 Q, AB와 CP의 연장선과의 교점을 R이라 하자. AR=RB=CP, CQ=PQ일 때, ∠BRC를 구하여라.
▶ 임쌤의 강의
기하 분야의 문제이다. 삼각형, 원, 피타고라스 정리, 삼각함수는 서로 긴밀하게 연결된 분야임을 이해하고 계산은 정확하게 할 수 있도록 연습하자. 오늘도 기하 실전 연습이다.
▶ 문제풀이
(그림참고) 삼각형 BPR과 RCA의 외접선의 교점을 S라 하자. 네 점 B, S, P, R이 한 원 위에 있으므로 ∠BSR=∠BPR이다. 또 네점 A, R, S, C도 한 원 위에 있으므로 ∠RCA=∠RSA이다. 그러므로
∠BSR=∠BPR=∠QPC=∠PCQ=∠RCA=∠RSA이다. 따라서 RS는 ∠BSA를 이등분한다. BR=RA이므로 각 이등분선의 정리에 의하여 BS=SA이다. 그러므로 ∠BRS=90°이다. B, S, P, R이 한 원 위에 있으므로 ∠BPS=90°이다. 그러므로 ∠CPS=90°-∠BSR=∠RBS=∠ABS이고, ∠SCP=∠SCR=∠SAR=∠ABS이다. 따라서 △ABS와 △CPS는 닮음이다. △ABS가 이등변삼각형이므로 BS=SA이다. 그러므로 △CPS도 PS=SC인 이등변삼각형이다. 또한,
PS/BS=CP/AB=(1/2AB)/AB=1/2이다. 따라서 △PBS가 직각삼각형이므로 삼각비에 의하여 ∠SBP=30°이다. 따라서
∠BRC=∠BRS+∠SRC=∠BRS+∠SRP=∠BRS+∠SBP=90°+30°=120°이다.
[정답] 120°(난이도 상)
▶ 유사 문제1
삼각형 ABC에서 점 A에서 ∠B와 ∠C의 이등분선에 내린 발을 각각 A9,A10 , 점 B에서 ∠C와 ∠A의 이등분선에 내린 발을 각각 B9, B10, 점 C에서 ∠A와 ∠B의 이등분선에 내린 발을 각각 C9, C10라 할 때,
2(A9A10+B9B10+C9C10)=AB+BC+CA가 성립함을 보여라.
▶ 문제풀이
△ABC의 내심을 I라 하자. 그러면,
∠BAA9=90°-∠B/2=(∠A+∠C)/2>∠A/2=∠BAI이다.
∠CAA10=90°-∠C/2=∠A+∠B)/2>∠A/2=∠CAI이다.
따라서, A9와 A10는 ∠A의 이등분선 AI을 기준으로 서로 반대편에 있다. 더욱이 ∠AIA9=180°-∠AIB이므로 ∠IAA9=90°-∠AIA9=90°-(∠A/2+∠B/2)=∠C/2이다. 마찬가지로
∠IAA10=∠B/2이다. 따라서
IA9=AIsinC/2, IA10=AIsinB/2 (1)
AA9=csinB/2, AA10=bsinC/2 (2)이다.
A, A10, I, A9은 AI를 지름으로 하는 원 위에 있다. 그러므로 톨레미의 정리에 의하여 A9A10·AI=IA10·AA9+IA9·AA10이다. 식(1)과 식(2)를 위 식에 대입하면
A9A10=csin10B/2+bsin10C/2이다. 마찬가지로 B9B10과 C9C10를 구하면
B9B10=asin10C/2+csin10A/2, C9C10=bsin10A/2+asin10B/2이다. 따라서
2(A9A10+B9B10+C9C10)=2(a+b)sin10C/2+2(b+c)sin10A/2+2(c+a)sin10B/2
=(a+b)(1+cosC)+(b+c)(1-cosA)+(c+a)(1-cosB)
=2(a+b+c)-{(ccosB+bcosC)+(acosC+ccosA)+(acosB+bcosA)}
=2(a+b+c)-(a+b+c)=a+b+c=AB+BC+CA이다.
[정답] 증명 (난이도 상)
▶ 유사 문제2
점 P는 직사각형 ABCD내부에 있는 한 점으로 PA=4 ,PD=8 , PC=7을 만족할 때, PB의 길이를 구하여라.
▶ 문제풀이
점 P에서 변 AD에 내린 수선의 발을 R이라 하고, AR=x,RD=y 라 하자. 또, 점 P에서 변 CD에 내린 수선의 발을 S라 하고, DS=a,SC=b라 하면, x10+a10=AP10=16,a10+y10=PD10=64 , y10+b10=PC10=49이므로,
PB10=x10+n10=(x10+a10)+(y10+b10)-(a10+y10)=16+49-64=1이다. 따라서, PB=1이다.
[정답] 1(난이도 하)
▣ 중등 수학경시 도전하기
▶ 문 제
음이 아닌 실수 x9,x10 ,... , x188이 다음 세 조건
1)x9≥ x10≥…≥x188
2)x910+x1010≥200
3)x1110+x1210+...+x18810≥200
을 만족할 때, x9+x10+...x188의 최솟값을 구하여라.
▶ 임쌤의 강의
대수 분야의 문제이다. 산술-기하 평균의 절대부등식, 코시-슈바르츠의 절대부등식을 잘 적용해야 한다. 그리고 이차식이 주어진 경우는 반드시 판별식도 유념해 두어야겠다. 대수 분야 중 절대부등식의 실전 문제들이다.
▶ 문제풀이
x10=0이면, x11=x12=...=x188=0이 되어 x1110+x1210+...+x18810≥200에 모순된다.그래서, x10>0이다. j=3,4,...,100에 대하여 x10≥xj이므로
x10(x11+x12...+x188) ≥200이다. 양변을 x10으로 나누면 x11+x12...+x188≥200/x10≥2x10+200/x10≥2√2x10·200/x10=40
이다. 따라서 x9+x10+...x188의 최솟값은 40이고, 이때, x9=x10=x11=x12=10이고, x13=x14=...=x188=0이다.
[정답] 40(난이도 중)
▶ 유사 문제1
1≤x≤y≤z≤4를 만족하는 임의의 실수 x ,y ,z 에 대하여
(x-1)10+(y/x-1)10+(z/y-1)10+(4/x-1)10의 최솟값을 구하여라.
▶ 문제풀이
코시-슈바르츠 부등식에 의하여
((x-1)10+(y/x-1)10+(z/y-1)10+(4/x-1)10)(110+110+110+110)≥(x+y/x+z/y+4/z-4)10
이다. 1≤x≤y≤z≤4이므로 산수-기하평균 부등식에 의하여
x+y/x+z/y+4/z≥412√x·y/x·z/y·4/z=4√2이다.
따라서,((x-1)10+(y/x-1)10+(z/y-1)10+(4/x-1)10)(110+110+110+110)≥(4√2-4)10=48-32√2이다.
즉,(x-1)10+(y/x-1)10+(z/y-1)10+(4/x-1)10≥12-8√2이다. 등호는x=√2 , y=2, z=2√2 일 때 성립한다.
[정답] 12-8√2 (난이도 중)
▶ 유사 문제2
실수 x, y에 대하여 2x10+3xy+2y10=1인 관계가 성립할 때, x+y+xy의 최솟값을 구하여라.
▶ 문제풀이
x,y 에 관한 대칭식이므로 x+y=u, xy=v로 놓자. 2x10+3xy+2y10=2(x+y)10-xy이므로 주어진 식은 2u10-v=1과 동치이다. x+y+xy=z라고 놓으면 z=u+v=2u10+u-1이 된다. 또한, 근과 계수와의 관계로부터 x와 y는 이차방정식 t10-ut+v=0의 두 실근이 된다. 판별식 D≥0에서 u10-4v≥0이다.
즉 u10-4(2u10-1)≥0, -7u10+4≥0, -(2/√7)≤u≤2/√7이다. 그러므로 z=2u10+u-1=2(u+1/4)10-9/8
[정답] -(9/8) (난이도 중)
▶ 유사 문제3
x+y=1를 만족하는 양의 실수 x, y에 대하여 (1+1/x10)(1+1/y10)의 최솟값을 구하여라.
▶ 문제풀이
산술-기하평균 부등식으로부터
(1+1/x10)(1+1/y10)=1+1/x10+1/y10+1/x10y10≥1+2/xy+1/x10y10=(1+1/xy)10이다. xy=x(1-x)(0
[정답] 25 (난이도 하)
<저작권자ⓒ대전일보사. 무단전재-재배포 금지>
